Welcome to Applied Maths Chapter 18, where we embark on an exciting journey into the world of advanced mathematical concepts tailored for Class 11 students.” Unlock the power of applied mathematics with expert solutions crafted by professionals at AppliedMath.com. Designed to propel students towards academic success, our meticulously curated ML Aggarwal Solutions for Applied Mathematics cater to Class 11 and Class 12 students seeking proficiency in their examinations. Every query from the CBSE ML Aggarwal Books finds a comprehensive answer on our platform, complete with detailed explanations and step-by-step solutions presented in an easily understandable language.
Dive into the world of applied mathematics and discover how our resources can elevate your understanding and performance. Keep reading to explore the wealth of ML Aggarwal Solutions for Class 11 and Class 12 Applied Mathematics.
Here we provide you with Applied Maths Chapter 18, to help you gain a comprehensive understanding of the chapter and its concepts. https://appliedmathsolution.com/wp-admin/post.php?post=6&action=edit

Applied Maths Chapter 18 Solutions
Circle And Parabola
EXERCISE- 18.3
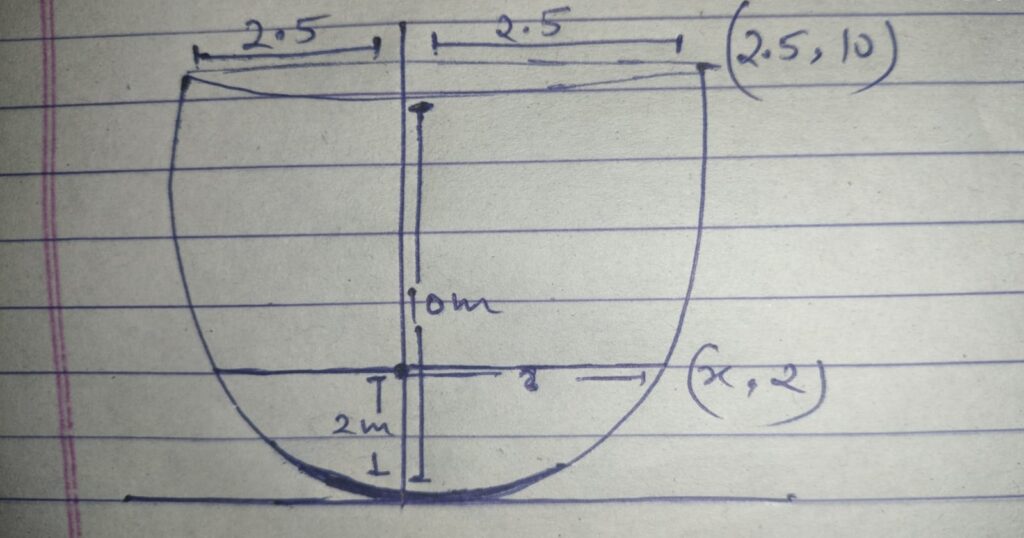
Q.1 An arc is in the form of a parabola with its axis vertically. The arc is 10 m high and 5 m wide at the base. How wide it is 2 m from the vertex of the parabola?
Ans. x^2 = 4ay
as it passes through (2.5,10)
(2.5)^2 = 4a x 10
6.25 = 40a
a = 6.25/40
Therefore, the equation of parabola
x^2 = 4 x 6.25/40y
x^2 = 6.25/10y
if y = 2
x^2 = 6.25/10 x 2
x^2 = 1.25
x = 1.12
Hence, the width of the parabola at 2m height = 1.12 x 2
= 2.24 m (approx)
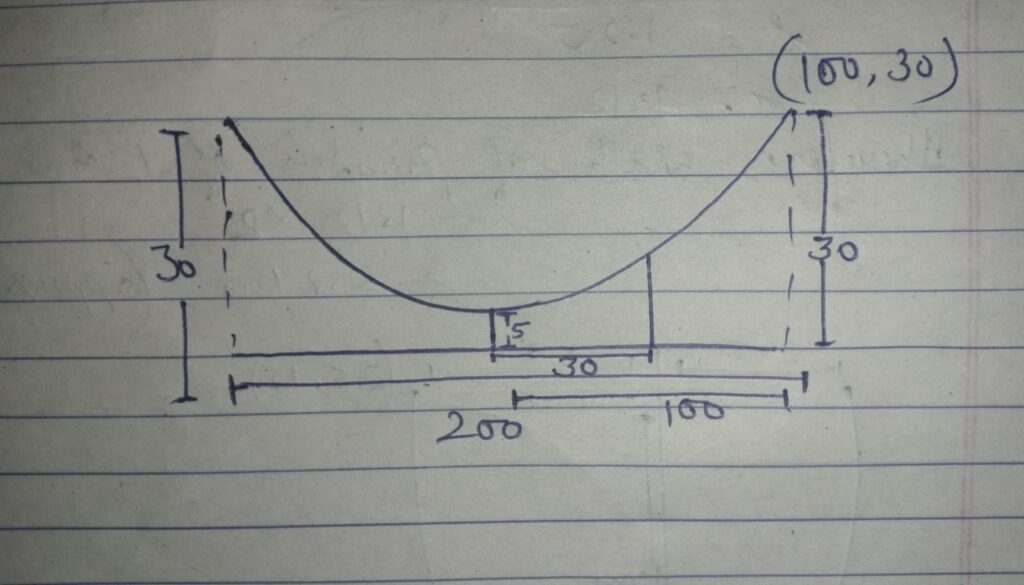
Q.2 The towers of a suspension bridge, hung in the form of a parabola, have their tops 30 metres above the roadway and are 200 metres apart. If the cable is 5 metres above the roadway at the centre of the bridge, find the length of the vertical supporting cable 30 metres from the centre.
Ans. Equation of parabola
x^2 = 4a (y-5)
(100)^2 = 4a (30 – 5)
10000 = 4a x 25
a = 100
Therefore,
Equation x^2 = 400 (y – 5)
if x = 30
(30)^2 = 400 (y – 5)
900/400 = y – 5
2.25 = y – 5
y = 7.25
Hence, the length of the wire = 7.25 m
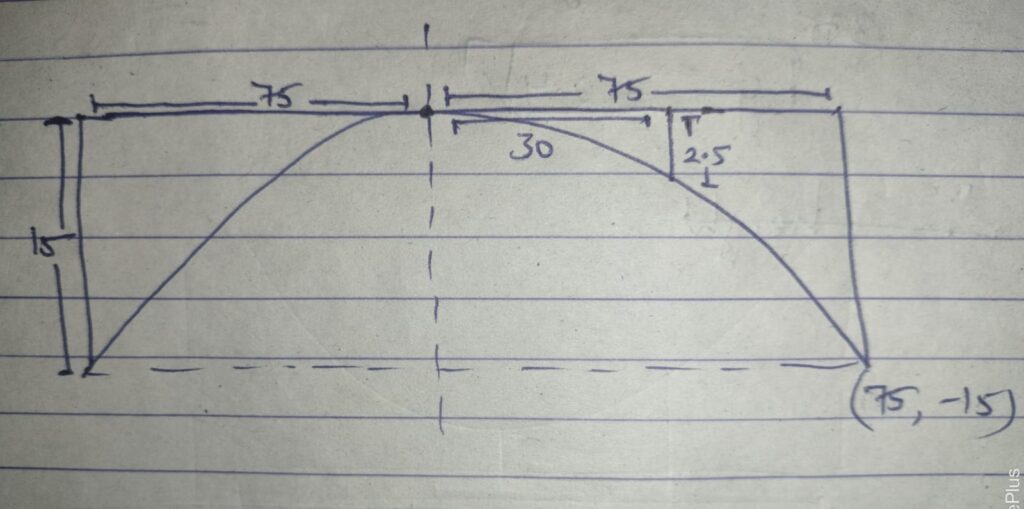
Q.3 The girder of a railway bridge is a parabola with its vertex at the highest point, 15 metres above the ends. If the span is 150 metres, find its height at 30 metres from the mid-point.
Ans. Equation of parabola
x^2 = -4ay
as it passes through (75, -15)
(75)^2 = -4a (- 15)
(75 x 75)/15 = 4a
4a = 375
Therefore,
Equation x^2 = -4ay
x^2 = -375y
if x = 30
(30)^2 = – 375y
900/375 = y
y = -2.4
Hence, height at 30m from midpoint = 15 – 2.4
= 12.6 m
FAQ’s related to Applied Maths Chapter 18 on Circle And Parabola:
Q.1 What is the equation of a circle and how is it derived?
Ans. The equation of a circle is (𝑥−ℎ)^2 + (𝑦−𝑘)^2= r^2, where (ℎ, 𝑘)(h, k) is the center of the circle and 𝑟 is the radius. This equation is derived from the distance formula between two points.
Q.2 What are the standard forms of the equation of a parabola?
Ans. The standard forms of the equation of a parabola are:
- Vertical Axis: 𝑦 = 𝑎𝑥^2 + 𝑏𝑥 + c
- Horizontal Axis: 𝑥 = 𝑎𝑦^2 + 𝑏𝑦 + 𝑐
These are few Frequently Asked Questions relating to Applied Maths Chapter 18
In Applied Maths chapter 18, you will explore fascinating topics that form the backbone of practical problem-solving techniques. Through clear explanations, illustrative examples, and step-by-step solutions, you’ll grasp complex concepts effortlessly. Whether you’re preparing for exams or simply eager to deepen your mathematical understanding, Applied Maths Chapter 18 promises an enriching learning experience that will set you on the path to success. Applied Maths Chapter 18, we delve deep into advanced mathematical concepts that are crucial for understanding.

